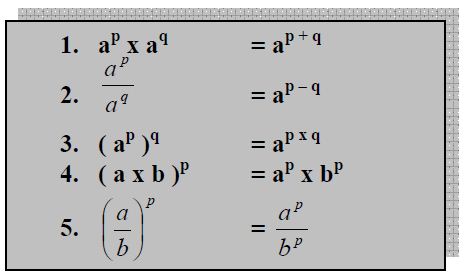
Materi eksponen ini saya bagi dalam empat sub bab, yaitu:
1. Sifat - sifat eksponen2. Persamaan eksponen
3. Pertidaksamaan eksponen
4. Fungsi eksponen
Mari kita bahas satu - persatu!
Catatan : tanda ^ menunjukkan pangkat!
1. Sifat - sifat Eksponen
1. a^n.a^m = a^(m+n)
2. a^n : a^m = a^(m-n)
3. (a^m)^n = a^mn
4. a^-n = 1 : a^n
5. a^0 = 1, a tidak nol
6. 1^n = 1
7. (ab)^n = a^n . b^n
8. (a : b)^n = a^n : b^n
9. akar pangkat n dari a^m = a^(m:n)
2. Persamaan Eksponen
1. a^f(x) = a^g(x)
f(x) = g(x)
2. h(x)^f(x) = h(x)^g(x)
* f(x) = g(x)
* h(x) = 1
* h(x) = -1, syarat : (-1)^f(x) = (-1)^g(x)
* h(x) = 0, syarat : f(x)>0, g(x)>0
3. a^f(x) = b^f(x)
f(x) = 0
4. a^f(x) = b^g(x)
log a^f(x) = log b^g(x)
f(x) log a = g(x) log b
dan seterusnya sampai di peroleh nilai x
5. A(a^f(x)^2 + B(a^f(x)) + C = 0, A,B,C elemen real, A
tidak nol
pemisalan : a^f(x) = p
A.p^2 + B.p + C = 0
faktorkan sampai diperoleh nilai p kemudian
di balikan ke x sehingga di dapat nilai x
3. Pertidaksamaan Eksponen
a^f(x) > a^g(x)
a > 1 maka f(x) > g(x)
0 < a < 1 maka f(x) < g(x)
4. Fungsi Eksponen
y = f (x) = a^x
a > 1
Sifat - sifat :
* monoton naik
* memotong sumbu-y di titik (0,1)
* kurva selalu di atas sumbu-x
* mempunyai asimtot y = 0
* x maks maka y maks
* x min maka y min
y = f (x) = a^x
0 < a < 1
Sifat - sifat :
* monoton turun
* memotong sumbu-y di titik (0,1)
* kurva selalu di atas sumbu-x
* mempunyai asimtot y = 0
* x maks maka y min
* x min maka y maks
Semoga bermanfaat.

Tidak ada komentar:
Posting Komentar